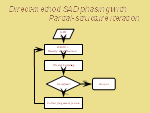
SIRAS treatment based on low-resolution SAD phasing
SIRAS phasing is important in solving membrane protein structures. Because anomalous
diffraction signals from intrinsic sulphur atoms are usually not enough to ensure a
successful SAD phasing while preperation of MIR specimens is often difficult.
In theory, diffraction phases can be derived from a set of protein SIRAS data without
ambiguity. However in practice, there may be imperfection of isomorphism between the
native protein and the heavy-atom derivative and, the high-resolution outoff of the
derivative may be much lower than that of the native. A case study on the treatment
of protein SIRAS data showed that effects of the above problems can be eliminated by the
SIRAS phasing starting from a low-resolution SAD phasing followed by a phase extension
from the derivative to the native
(more details).
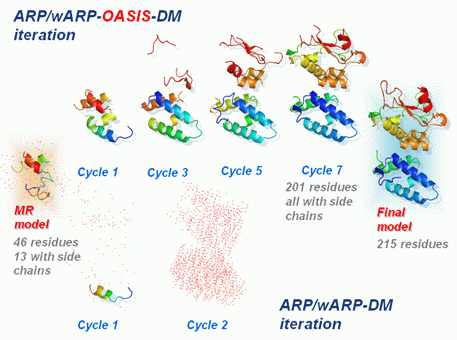
The known protein TTHA1012 with 213-residues was solved in a test of the pipeline
IPCAS based on
the anomalous scattering signals from 2 sulphur atoms under Cr-Kα radiation.
Ten cycles iterative SAD phasing were performed uisng the programs
OASIS, DM, RESOLVE
(build only) and ARP/wARP. The resultant best model (shown on the left of the following figure)
consists of 166 residues (166 of which sequenced) with R/Rfree=0.267/0.343.
Based on this model, ten cycles of iterative fragment extension running with OASIS, DM
and Buccaneer led to a model (on the right of the following figure) containing 200 residues
(198 of which sequenced) with R/Rfree=0.246/0.303.
2012
OASIS (v4.2) - IPCAS (v1.0) released
OASIS 4.2 - a program of direct-method phasing based on a partial model with or
without SAD/SIR information;
2010
I. New expression of bimodal SAD-phase distributions by the sum of two von Mises
distributions
IPCAS 1.0 - a pipeline for "Iterative Protein
Crystal-structure Automatic Solution" developed in
the
"Institute of Physics, Chinese
Academy of Sciences".
An important step in direct-method SAD phasing is to express SAD-phase distributions by the sum of two unimodal distributions. Up to the moment, Guassian distribution has been used for this purpose in the program OASIS. However this could cause large errors when Δφ is small. Much better results can be obtained by replaceing the Guassian distribution with the von Mises distribution. In the following figure the solid line denotes the experimental bimodal phase distribution; Black dots indicate the approximation by the sum of two von Mises distributions; Blank diamonds indicate the approximation by the sum of two Gaussian distributions. As is seen the von Mises approaximation is much better than the Guassian one. The new expression will be used in the next version of OASIS. Click on the figure to read the original publication.
II. Combination of SAD- and MR-iteration
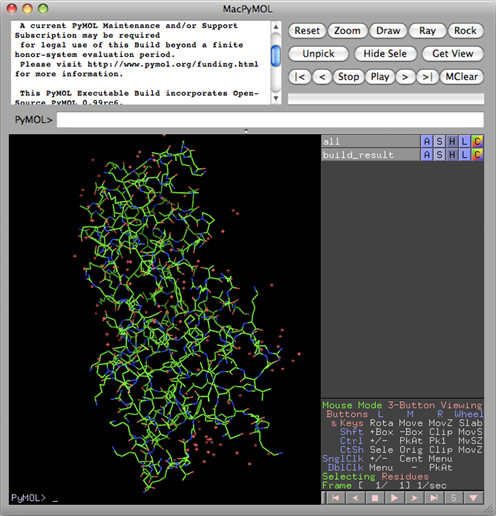
Ribbon structure models of TTHA1012 plotted by PyMOL are shown in the following figure. Left: the best model from cycles 0-20 of SAD iteration; Right: the best model from 1-10 cycles MR iteration based on 0-10 cycles SAD iteration. As is seen the result from SAD+MR iteration is better than that from SAD iteration alone. Click on the figure to read the original publication.
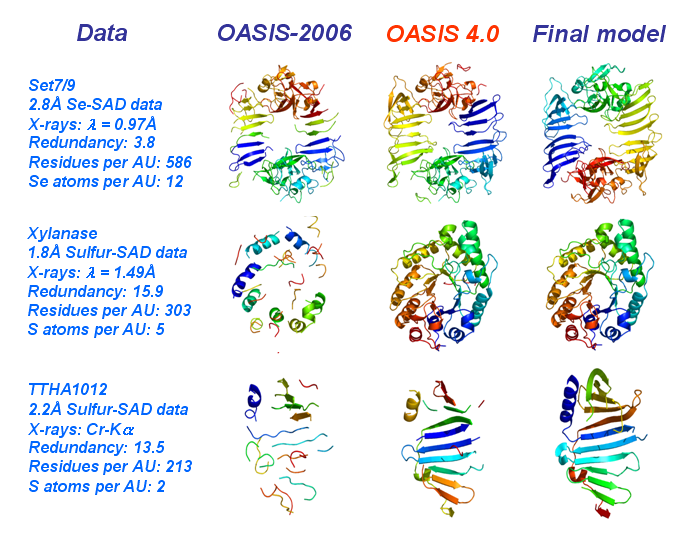
New version of OASIS: OASIS4.0
I. Improved SAD phasing
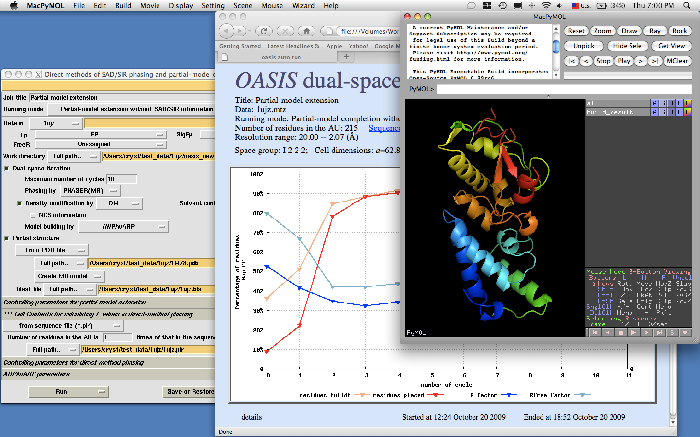
II. GUI for controlling and monitoring OASIS dual-space iteration
Control panel
Monitoring board
Details for finished cycles
Real-time model display
Detailed description of the OASIS GUI
I. Combining SOLVE/RESOLVE with OASIS/DM at low resolution
2007
Click on the map for a summary of the sample
II. SAD phasing and fragment extension at different resolutions down to 3Å and below
Click on the map for a summary of the sample
References:
[1] Y. He, Y.X. Gu, Z.J. Lin, C.D. Zheng and H.F. Fan,
Chinese Physics 16, 3022-3028. (2007)
[2] D.Q. Yao, H. Li, Q. Chen, Y.X. Gu, C.D. Zheng, Z.J. Lin, H.F. Fan, N. Watanabe and B.D. Sha,
Chinese Physics B 17, 0-0 (2008)
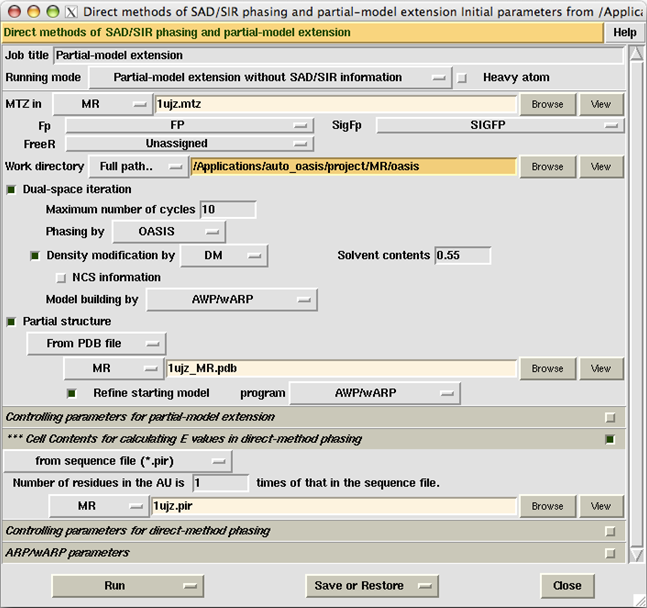
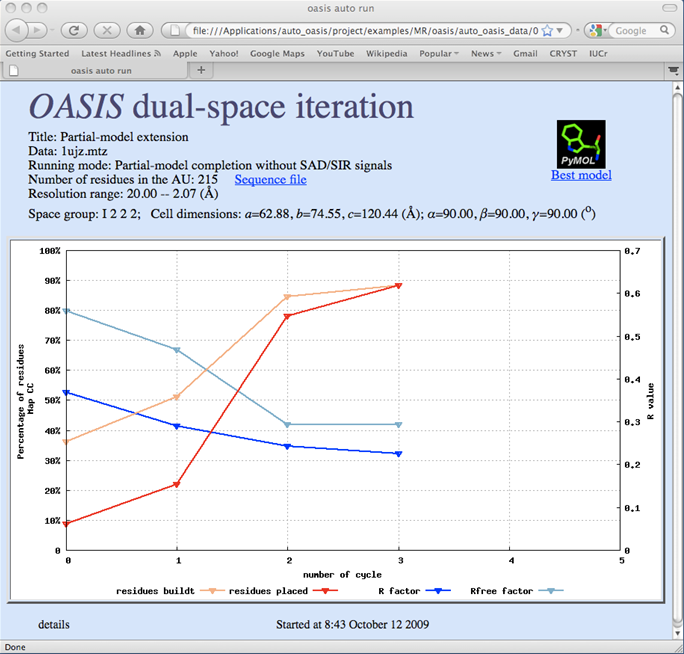
Direct-method dual-space fragment extension for MR model completion
The direct-method dual-space fragment extension has been extended to use in the case where SAD/SIR information are not available. Test with the protein 1UJZ showed that the technique is very efficient in model completion starting with a partial structure (~20% of the total) obtained from molecular replacement.
Reference:
Y. He, D.Q. Yao, Y.X. Gu, Z.J. Lin, C.D. Zheng & H.F. Fan,
Acta Cryst. D63, 793-799. (2007)
Dual-space fragment extension using SAD data
Extensive case studies have been carried out. Results have been summarized in References.
| Flow chart | Azurin | Lysozyme | Xylanase |
|
|
|
|
References:
[1] D.Q. Yao, S. Huang, J.W. Wang, Y.X. Gu, C.D. Zheng & H.F. Fan, N. Watanabe & I. Tanaka,
Acta Cryst. D62, 883-890. (2006)
[2] N. Watanabe, Y. Kitago, I. Tanaka, J.W. Wang, Y.X. Gu, C.D. Zheng & H.F. Fan,
Acta Cryst. D61, 1533-1540. (2005)
I. Auto-tuning the error term in direct-method SAD phasing
The probability formula of direct-method SAD phasing used in the program OASIS contains an error term, which is related to the lack-of-closure error. Previously in the error term, there is a constant to be determined empirically for each particular case. It has been found that improper choice of the constant led often to the failure of phase derivation. The problem is resolved by introducing a modified error term and a method of automatically tuning the associated scaling factor.
Electron density maps obtained by a default run of the modified OASIS followed by a default run of DM (Cowtan, K.).
| Cu-SAD | S-SAD | Se-SAD | Br-SAD |
|
|
|
|
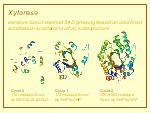
II. Direct-method SAD phasing with reciprocal-space fragment extension
Structure fragments obtained from automatic model building based on direct-method SAD phasing are fed back to the direct-method probability formula to strengthen the phasing power and to benefit automation.
| Flowchart | Xylanase synchrotron S-SAD data | ||
|
|
|
|
| Rusticyanin synchrotron Cu-SAD data | Thaumatin Cr-Ka S-SAD data | ||
|
|
|
|
References:
[1] J.W. Wang, J.R. Chen, Y.X. Gu, C.D. Zheng, F. Jiang and H.F. Fan,
Acta Cryst. D60, 1987-1990. (2004)
[2] J.W. Wang, J.R. Chen, Y.X. Gu, C.D. Zheng, and H.F. Fan,
Acta Cryst. D60, 1991-1996. (2004)
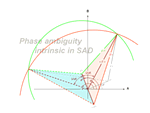
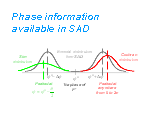
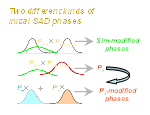
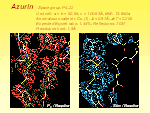
SAD phasing, why direct methods?
SAD phasing is becoming popular in solving protein structures. The essential point to success is to break the phase ambiguity intrinsic in SAD data. Mostly this is done using density-modification techniques. However, density modification does not directly make choice between the two possible SAD phases for each reflection. The use of density-modification techniques alone leads often not to the best results. Two kinds of phase information enable discrimination of phase doublets from SAD data. One is from the heavy atoms (anomalous scatterers), while the other from the phase relationship of direct methods. The former can be expressed by the Sim distribution, while the latter can be expressed by the Cochran distribution. Usually only the Sim distribution is used to yield initial phases for the subsequent density modification. We use instead the product of the Sim and the Cochran distributions to produce initial phases, which have been proved much better than that from only the Sim distribution. Density modification based on such phases has been proved capable of yielding much better results than that based on only the Sim distribution.
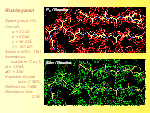
Comparison of SAD phasing with and without direct methods
| Phase ambiguity intrinsic in SAD | Phase information available in SAD | Two different kinds of initial SAD phases | Phase probability disributions |
|
|
|
|
| Cumulative phase errors |
HMT SET7/9 | Rusticyanin | Azurin |
|
|
|
|
Reference:
[1] J.W. Wang, J.R. Chen, Y.X. Gu, C.D. Zheng, F. Jiang, H.F. Fan, T.C. Terwilliger
and Q. Hao, Acta Cryst. D60, 1244-1253. (2004)
)
|
2002: Conventional MIR phases of the known protein Rpe have been significantly improved by the direct-method procedure DMIR Y.X. Gu, W.R. Chang, T. Jiang, C.D. Zheng & H.F. Fan, Acta Cryst. A58, 547-551 (2002)
|
)
|
2001: The Fourier map from conventional MAD phasing of 4-wavelength anomalous diffraction data was improved by direct-method phasing of only the 2-wavelength subset of data Fan Hai-fu, lecture at the Euro Conference on Phasing Biological Macromolecules, Martina Franca, Italy, June 2001 
Y.X. Gu, F. Jiang, B.D. Sha & H.F. Fan, Z. Krist. 217, 710-714 (2002)
|
)
|
2001: Direct-method aided MAD phasing --- the first example of improving MAD phases by direct methods Y.X. Gu, Y.D. Liu, Q. Hao. S.E. Ealick & H.F. Fan, Acta Cryst. D57, 250-253 (2001)
|
| OASIS | 2000: The CCP4 supported program for direct-method phasing of One-wavelength Anomalous Scattering or Single Isomorphous Substitution (replacement) Data Hao, Q., Gu, Y.X., Zheng, C.D. & Fan, H.F., J Appl. Cryst. 33, 980-981 (2000)
|
)
|
1999: The first example of breaking the protein SIR phase ambiguity when replacing atoms are in centric arrangement Liu Yu-dong, Gu Yuan-xin, Zheng Chao-de, Q. Hao and Fan Hai-fu, Acta Cryst. D55, 846-848 (1999)
|
)
|
1999: Comparing the result of breaking SAD-phase ambiguity using direct methods and that without using direct methods Liu Yu-dong, I. Harvey, Gu Yuan-xin, Zheng Chao-de, He Yi-zong, Fan Hai-fu, S. S. Hasnain, and Q. Hao, Acta Cryst. D55, 1620-1622 (1999)
|
)
|
1997: The first example of solving an originally unknown protein by direct-method phasing of the 2Å SAD data H. F. Fan, Q. Hao, I. Harvey, S. S. Hasnain, Y. D. Liu, Y. X. Gu, C. D. Zheng & H. Ke, in "Direct Methods for Solving Macromolecular Structures" Ed. by S. Fortier, Kluwer Academic Publishes, The Netherlands, 1998, pp. 479-485.
|
)
|
1996: Direct-method phasing and solvent flattening treatment of the 1.9Å SAD data of the protein azurin led to an easily traceable Fourier map Zheng Xiao-feng, Fan Hai-fu, Q. Hao, F.E. Dodd & S.S. Hasnian, Acta Cryst. D52, 937-941 (1996)
|
)
|
1995:
Test with the SAD data from the protein core streptavidin, which was originally solved using 3-wavelength MAD data Sha Bing-dong, Liu Shen-ping, Gu Yuan-xin, Fan Hai-fu, Hengming Ke, Yao Jia-xing & M. M. Woolfson, Acta Cryst. D51, 342-346 (1995)
|
)
|
1990:
The first traceable Fourier map from direct-method phasing of the experimental 2Å SAD data of the protein aPP Fan Hai-fu, Hao Quan, Gu Yuan-xin, Qian Jin-zi, Zheng Chao-de & Hengming Ke, Acta Cryst. A46, 935-939 (1990)
|
| 1988:
The first successful test on direct-method phasing of the 3Å experimental SIR data from the native Bence Jones protein Rhe and its Au-derivative Collaborative work by H.F. Fan and B.C. Wang, 1988 (see M.M. Woolfson and Fan, Hai-fu, Physical and Non-physical Methods of Solving Crystal Structures, Cambridge University Press, 1995. Pp. 164-166.) 
|
|
| 1985:
The first successful test on direct-mothod phasing of the 2Å experimental SAD data from the protein aPP Fan Hai-fu & Gu Yuan-xin, Acta Cryst. A41, 280-284 (1985)
|
|
| 1965:
It was proposed that the phase ambiguity due to single-wavelength anomalous diffration (SAD) or single isomorphous replacement (SIR) could be resolved by direct methods. Fan Hai-fu, Chinese Phys. 1429-1435 (1965)
 see also
Fan Hai-fu, Acta Phys. Sin. 21 1114-1118 (1965). (In Chinese)
|